Introduction

A linear regression model with \(k\) regressors

\[\label{eq1} \mathbf{y}=\mathbf{X}\beta+\mathbf{u}\]

where \(y\) and \(u\) are \(n-\)vectors, \(X\) is an \(n\times k\) matrix, and \(\beta\) is a \(k-\)vector.

\[\begin{eqnarray} \label{eq2} y&=&\left[\begin{array}{c} y_{1}\\ y_{2}\\ \vdots\\ y_{n} \end{array} \right], \beta=\left[\begin{array}{c} \beta_{1}\\ \beta_{2}\\ \vdots\\ \beta_{k} \end{array} \right], u=\left[\begin{array}{c} u_{1}\\ u_{2}\\ \vdots\\ u_{n} \end{array} \right], \end{eqnarray}\] \[\begin{eqnarray} \label{eq3} X&=&\left[\begin{array}{cccc} X_{11}&X_{12}&\cdots&X_{1k}\\ X_{21}&X_{22}&\cdots&X_{2k}\\ \vdots&\vdots&&\vdots\\ X_{n1}&X_{n2}&\cdots&X_{nk} \end{array} \right] \end{eqnarray}\]

A typical row of this equation is

\[\begin{eqnarray} \label{eq4} y_{t}&=&X_{t}\beta+u_{t}=\sum_{i=1}^{k}\beta_{i}X_{ti}+u_{t} \end{eqnarray}\]

where \(X_{t}\) denotes the \(t^{th}\) row of \(X\) OLS estimates of the vector \(\beta\) are \(\label{eq5} \hat{\beta}=(X^{T}X)^{-1}X^{T}y\)

numerical properties: properties of estimates if they have nothing to do with how the data were actually generated. Such properties hold for every set of data by virtue of the way in which \(\hat{\beta}\) is computed, and the fact that they hold can always be verified by direct calculation.
statistical properties: depend on unverifiable assumptions about how the data were generated, and they can never be verified for any actual data set.

The Geometry of OLS Estimation

We partition \(X\) in terms of its columns as follows,

\[\begin{eqnarray*} X&=&\left[\begin{array}{cccc} x_{1}&x_{2}&\cdots&x_{k} \end{array} \right] \end{eqnarray*}\]

is just a linear combination of the columns of \(X\).

Then we find that

\[\begin{eqnarray*} X\beta&=&\left[\begin{array}{cccc} x_{1}&x_{2}&\cdots&x_{k} \end{array} \right]\left[\begin{array}{c} \beta_{1}\\ \beta_{2}\\ \vdots\\ \beta_{k} \end{array} \right]\\ &=&x_{1}\beta_{1}+x_{2}\beta_{2}+\dots+x_{k}\beta_{k}=\sum_{i=1}^{k}\beta_{i}x_{i} \end{eqnarray*}\]

Any \(n\)-vector \(X\beta\) belongs to \(S(x)\), which is a \(k\)-dimensional subspace of \(E^{n}\). In particular, the vector \(X\hat{\beta}\) constructed using the OLS estimator \(\hat{\beta}\) belongs to this subspace.

The estimator \(\hat{\beta}\) was obtained by solving the equation (\ref{eqp8}).

\[\begin{eqnarray} \label{eqp8} X^{T}(y-X\hat{\beta})&=&0 \end{eqnarray}\]

We select a single row of matrix product in (\ref{eqp8}), the \(i^{th}\) element is

\[\begin{eqnarray} \label{eqp9} x^{T}_{i}(y-X\hat{\beta})&=&\langle x^{T}_{i},y-X\hat{\beta}\rangle=0 \end{eqnarray}\]

(\ref{eqp9}) means that the vector \(y-X\hat{\beta}\) is orthogonal to all of the regressors \(x_{i}\). As a result, (\ref{eqp8}) is referred to as orthogonality conditions

(\ref{eqp9}) also means that \(\hat{u}\) is orthogonal to all the regressors, which implies that \(\hat{u}\) is orthogonal to every vector in \(S(X)\), the span of the regressors.

The vector \(X\hat{\beta}\) is referred to as the vector of fitted values, and it lies in \(S(X)\). Consequently, \(X\hat{\beta}\) must be orthogonal to \(\hat{u}\).

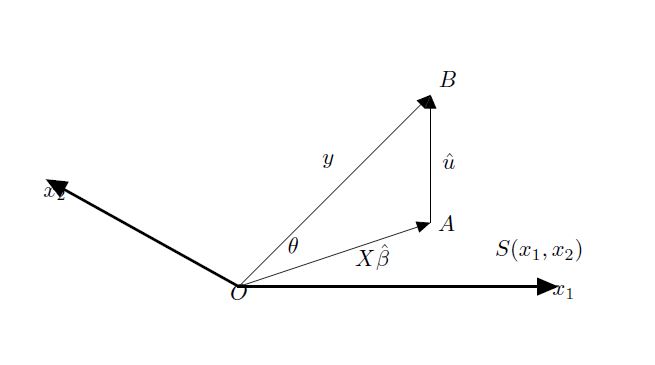
Linear regression in three dimensions

From Figure we observe that the shortest distance from \(y\) to the horizontal plane is obtained by descending vertically on to it, and the point in the horizontal plane vertically below \(y\) , labeled \(A\) in the figure, is the closest point in the plane to \(y\). Thus \(\|\hat{u}\|\) minimizes \(\|u(\beta)\|\).

We can see that \(y\) is the hypotenuse of the triangle, the other two sides being \(X\hat{\beta}\) and \(\hat{u}\). We have

\[\begin{eqnarray} \label{eqp10} \|y\|^{2}&=&\|X\hat{\beta}\|^{2}+\|\hat{u}\|^{2} \end{eqnarray}\]

We can rerwrite it as scalar products

\(\begin{eqnarray} \label{eqp11} y^{T}y&=&\hat{\beta}^{T}X^{T}X\hat{\beta}+(y-X\hat{\beta})^{T}(y-X\hat{\beta}) \end{eqnarray}\) The total sum of squares(TSS) is equal to the explained sum of squares(ESS) plus the sum of squared residuals(SSR)

Orthogonal Projections

When we estimate a linear regression model, we map the regressand \(y\) into a vector of fitted \(X\hat{\beta}\) and a vector of residuals \(\hat{u}=y-X\hat{\beta}\). These mappings are examples of orthogonal projections.

A projection is a mapping that takes each point of \(E^{n}\) into a point in a subspace of \(E^{n}\), while leaving all points in that subspace unchanged. An orthogonal projection maps any point into the point of the subspace that is closest to it.

An orthogonal projection on to a given subspace can be performed by premultiplying the vector to be projected by a suitable projection matrix. In OLS, we use the following two projections matrices that yield the vector of fitted values and the vector of residuals

\[\begin{eqnarray} \label{eqp12} P_{X}&=&X\left(X^{T}X\right)^{-1}X^{T}\\ \nonumber M_{X}&=&I-P_{X}=I-X\left(X^{T}X\right)^{-1}X^{T} \end{eqnarray}\]

Properties

\[\begin{eqnarray} \label{eqp13} X\hat{\beta}&=&X(X^{T}X)^{-1}X^{T}y=P_{X}y\\\nonumber \hat{u}&=&y-X\hat{\beta}=(I-P_{X})y=M_{X}y \end{eqnarray}\]
(\ref{eqp13}) says that projection matrix \(P_{X}\) projects on to \(S(X)\). For any \(n-\)vector \(y\), \(P_{X}y\) always lies in \(S(X)\).

The image of \(P_{X}\), which is a shorter name for its invariant subspace, is precisely \(S(X)\). The image of \(M_{X}\) is \(S^{\bot}(X)\), the orthogonal complement of image of \(P_{X}\).
Symmetric and idempotent
\[\begin{eqnarray*} P_{X}^{T}&=&P_{X}\\ P_{X}P_{X}&=&P_{X}\\ M_{X}^{T}&=&M_{X}\\ M_{X}M_{X}&=&M_{X} \end{eqnarray*}\]
We can think that project a vector it on to \(S(X)\), and then project it on to \(S(X)\) again, the second projection has no effect at all. So it is left unchanged. For any vector \(y\), we have
\[\begin{eqnarray} \label{eqp17} P_{X}P_{X}y&=&P_{X}y \end{eqnarray}\]
\[\begin{eqnarray*} P_{X}X&=&X\\ M_{X}X&=&0 \end{eqnarray*}\]
\(P_{X}\) and \(M_{X}\) annihilate each other
\[\begin{eqnarray} \label{eqp19} P_{X}M_{X}&=&0 \end{eqnarray}\]
The projection matrix \(M_{X}\) annihilates all points that lie in \(S(X)\), and \(P_{X}\) likewise annihilates all points that lie in \(S^{\bot}(X)\).
\[X=\left[\begin{array}{cc} x_{1}&x_{2} \end{array}\right]\] \[\begin{eqnarray*} P_{x_{1}}&=&P_{X}\\ P_{x_{1}}P_{X}&=&P_{X}P_{x_{1}}=P_{x_{1}}\\ M_{x_{1}}&=&M_{X}\\ M_{x_{1}}M_{X}&=&M_{X}M_{x_{1}}=M_{X} \end{eqnarray*}\]
Pythagoras’ Theorem
\[\begin{eqnarray*} \left\lVert y \right\rVert^{2}&=&\left\lVert P_{X}y \right\rVert ^{2}+\left\lVert M_{X}y \right\rVert^{2} \end{eqnarray*}\]

Linear Transformations of Regressors

If \(A\) is any nonsingular \(k\times k\) matrix, we postmultiply \(X\) by \(A\). It is called a nonsingular linear transformation

\[\begin{eqnarray*} XA&=&X\left[\begin{array}{cccc} a_{1}&a_{2}&\cdots&a_{k} \end{array}\right]\\ &=&\left[\begin{array}{cccc} Xa_{1}&Xa_{2}&\cdots&Xa_{k} \end{array}\right] \end{eqnarray*}\]

where \(Xa_{i}\) is an \(n-\)vector that is a linear combination of columns of \(X\). Thus any element of \(S(XA)\) must be an element of \(SX\). Any element of \(S(X)\) is also an element of \(S(XA)\). So these two subspaces must be identical. As a result, the orthogonal projections \(P_X\) and \(P_{XA}\) should be same.

\[\begin{eqnarray*} P_{XA}&=&XA\left(A^{T}X^{T}XA\right)^{-1}A^{T}X^{T}\\ &=&XAA^{-1}(X^{T}X)^{-1}(A^{T})^{-1}A^{T}X^{T}\\ &=&X(X^{T}X)^{-1}X^{T}=P_{X} \end{eqnarray*}\]

We have known that the vectors of fitted values and residuals depend on \(X\) only through \(P_{X}\) and \(M_{X}\). Therefore, they too must be invariant to any nonsingular linear transformation of the columns of \(X\).

If we replace \(X\) by \(XA\) in the regression \(y=X\beta+u\), the residuals and fitted values will not change, even though \(\hat{\beta}\) will change.

The Frisch-Waugh-Lovell Theorem

Consider the following two regressions

\[\begin{eqnarray} \label{eq20} y&=&X_{1}\beta_{1}+X_{2}\beta_{2}+u\\ \label{eq21} M_{1}y&=&M_{1}X_{2}\beta_{2}+M_{1}u \end{eqnarray}\]

::: proposition Frisch-Waugh-Lovell Theorem

The OLS estimates of \(\beta_{2}\) from regressions (\ref{eq20}) and (\ref{eq21}) are numerically identical.
The residuals from regressions (\ref{eq20}) and (\ref{eq21}) are numerically identical. :::

Let \(\hat{\beta_{2}}\) be the estimates of regression (\ref{eq20}) and \(\widetilde{\beta_{2}}\) be the estimates of regression (\ref{eq21})

::: proof Proof. We define \(\hat{\beta_{2}}\) is the OLS estimator for \(\beta_{2}\) in (\ref{eq20}) and \(\tilde{\beta_{2}}\) is the OLS estimator for \(\beta_{2}\) in (\ref{eq21}). We let \(\hat{u}\) be the residual for (\ref{eq20}) and \(\tilde{u}\) for (\ref{eq21}).

First we prove result 1.

\[\begin{eqnarray*} \tilde{\beta_{2}}&=&\left((M_{1}X_{2})^{T}M_{1}X_{2}\right)^{-1}(M_{1}X_{2})^{T}M_{1}y\\ &=&\left(X_{2}^{T}M_{1}X_{2}\right)^{-1}X_{2}^{T}M_{1}y\\ &=&\left(X_{2}^{T}M_{1}X_{2}\right)^{-1}X_{2}^{T}M_{1}(X_{1}\hat{\beta_{1}}+X_{2}\hat{\beta_{2}}+M_{X}y)\\ &=&\left(X_{2}^{T}M_{1}X_{2}\right)^{-1}X_{2}^{T}M_{1}X_{2}\hat{\beta_{2}}+X_{2}^{T}M_{1}M_{X}y\\ &=&\left(X_{2}^{T}M_{1}X_{2}\right)^{-1}X_{2}^{T}M_{1}X_{2}\hat{\beta_{2}}+X_{2}^{T}M_{X}y\\ &=&\left(X_{2}^{T}M_{1}X_{2}\right)^{-1}X_{2}^{T}M_{1}X_{2}\hat{\beta_{2}}+(M_{X}X_{2})^{T}y\\ &=&\hat{\beta_{2}} \end{eqnarray*}\]

Then we prove result 2

\[\begin{eqnarray*} M_{1}y&=&M_{1}(X_{1}\hat{\beta_{1}}+X_{2}\hat{\beta_{2}}+M_{X}y)\\ &=&M_{1}X_{2}\hat{\beta_{2}}+M_{X}y\\ &=&M_{1}X_{2}\tilde{\beta_{2}}+M_{X}y\\ &=&M_{1}X_{2}\tilde{\beta_{2}}+\hat{u}\\ \end{eqnarray*}\]

We know \(M_{1}y=M_{1}X_{2}\tilde{\beta_{2}}+\tilde{u}\)

Thus we have \(\tilde{u}=\hat{u}\) :::

Applications of FWL Theorem

Goodness of Fit of a Regression

\[\begin{eqnarray*} TSS=\left\lVert y \right\rVert^{2}&=&\left\lVert P_{X}y \right\rVert ^{2}+\left\lVert M_{X}y \right\rVert ^{2}=ESS+SSR \end{eqnarray*}\]

And we can define the goodness of fit for a regression model. The measure is referred to as the \(R^{2}\)

\[\begin{eqnarray} \label{eqfwl3} R^{2}_{u}&=&\frac{ESS}{TSS}=\frac{\left\lVert P_{X}y \right\rVert ^{2}}{\left\lVert y \right\rVert^{2}}=1-\frac{\left\lVert M_{X}y\right\rVert^{2}}{\left\lVert y\right\rVert^{2}}=1-\frac{SSR}{TSS}=\cos \theta ^{2} \end{eqnarray}\]

The \(R^{2}\) defined in (\ref{eqfwl3}) is called the uncentered \(R^{2}\). It is invariant under nonsingular linear transformations of the regressors, e.g. the changes in the scale of \(y\) (the angle \(\theta\) remains same). However, it will change when the changes of units change the angle \(\theta\).

We define the centered \(R^{2}\)

\[\begin{eqnarray} \label{eqfwl4} R^{2}_{c}&=&\frac{\left\lVert P_{X}M_{\iota}y\right\rVert^{2}}{\left\lVert M_{\iota}y\right\rVert^{2}}=1-\frac{\left\lVert M_{X}y\right\rVert^{2}}{\left\lVert M_{\iota}y\right\rVert^{2}} \end{eqnarray}\]

Influential Observations and Leverage

One or a few observations in a regression are highly influential, in the sense that deleting them from the sample would change some elements of \(\hat{\beta}\) substantially.

Leverage

The effect of a single observation on \(\hat{\beta}\) can be seen by comparing \(\hat{\beta}\) with \(\hat{\beta}^{t}\), the estimate of \(\beta\) that would be obtained if the \(t^{th}\) observation were omitted from the sample.

Let

\[e_{t}=\left[\begin{array}{ccccccc} 0&\cdots&0 &1&0&\cdots&0 \end{array}\right]^{T}\]

is n \(n\)-vector which has \(t^{th}\) element 1 and all other element 0. Including \(e_{t}\) as a regressor

\[\begin{eqnarray} \label{eq22} y&=&X\beta+\alpha e_{t}+u \end{eqnarray}\]

By FWL,

\[\begin{eqnarray} \label{eq23} M_{t}y&=&M_{t}X\beta+residuals \end{eqnarray}\]

where \(M_{t}=M_{e_{t}}=I-e_{t}(e_{t}^{T}e_{t})^{-1}e_{t}^{T}\). It is easy to find

\[\begin{eqnarray*} M_{t}y&=&y-e_{t}(e_{t}^{T}e_{t})^{-1}e_{t}^{T}y=y-e_{t}e_{t}^{T}y=y-y_{t}e_{t} \end{eqnarray*}\]

Thus \(y_{t}\) is subtracted from \(y\) fro the \(t^{th}\) observation only. Similarly, \(M_{t}X\) is just \(X\) with its \(t^{th}\) row replaced by zeros. Therefore, running (\ref{eq23}) will give the same parameter estimates as those that would be obtained if we deleted observation \(t\) from the sample.

Let \(P_{Z}\) and \(M_{Z}\) be the orthogonal projections on to and off \(S(X,e_{t})\).

\[\begin{eqnarray} \label{eq24} y&=&P_{Z}y+M_{Z}y=X\hat{\beta}^{t}+\hat{\alpha}e_{t}+M_{Z}y \end{eqnarray}\]

Premultiply by \(P_{X}\)

\[\begin{eqnarray*} P_{X}y&=&X\hat{\beta}^{t}+\hat{\alpha}P_{X}e_{t} \end{eqnarray*}\]

So we have

\[\begin{eqnarray*} X\hat{\beta}&=&X\hat{\beta}^{t}+\hat{\alpha}P_{X}e_{t}\\ X(\hat{\beta}^{t}-\hat{\beta})&=&-\hat{\alpha}P_{X}e_{t} \end{eqnarray*}\]

Now we need to calculate \(\hat{\alpha}\). By FWL, from (\ref{eq22}) we get

\[\begin{eqnarray*} M_{X}y&=&\hat{\alpha}M_{X}e_{t}+residuals \end{eqnarray*}\]

and we have

\[\begin{eqnarray*} \hat{\alpha}&=&((M_{X}e_{t})^{T}M_{X}e_{t})^{-1}(M_{X}e_{t})^{T}M_{X}y\\ &=&\frac{e_{t}^{T}M_{X}y}{e_{t}^{T}M_{X}e_{t}} \end{eqnarray*}\]

where \(e_{t}^{T}M_{X}y\) is the \(t^{th}\) element of \(M_{X}y\) and we denote this element as \(\hat{u}_{t}\). Similarly, \(e_{t}^{T}M_{X}e_{t}\) is the \(t^{th}\) diagonal element of \(M_{X}\). So we have

\(\begin{eqnarray} \label{eq25} \hat{\alpha}&=&\frac{\hat{u}_{t}}{1-h_{t}} \end{eqnarray}\) where \(h_{t}\) is the \(t^{th}\) diagonal element of \(P_{X}\).

So we have

\[\begin{eqnarray*} X(\hat{\beta}^{t}-\hat{\beta})&=&-\hat{\alpha}P_{X}e_{t}\\ (X^{T}X)^{-1}X^{T}X(\hat{\beta}^{t}-\hat{\beta})&=&-\frac{\hat{u}_{t}}{1-h_{t}}(X^{T}X)^{-1}X^{T}P_{X}e_{t}\\ \hat{\beta}^{t}-\hat{\beta}&=&-\frac{\hat{u}_{t}}{1-h_{t}}(X^{T}X)^{-1}X^{T}P_{X}e_{t}\\ &=&-\frac{\hat{u}_{t}}{1-h_{t}}(X^{T}X)^{-1}X^{T}_{t}\hat{u}_{t} \end{eqnarray*}\]